Canvas与贝塞尔曲线初探

Canvas简介

HTML5提供了一些新的功能，可以实现许多令人惊叹不已的效果。
而Canvas便是其中一个极为有用的功能，它能通过JavaScript来绘制图形，可以画图，合成照片，创建动画甚至实时视频处理与渲染。

本文将会介绍一些用Canvas创建简单动画的方法。

如何使用Canvas

<canvas>是 HTML5 新增的元素想要使用Canvas进行绘图，首先需要在HTML中加入如下标签

<canvas id="canvas"></canvas>

然后再添加以下JavaScript代码

var canvas = document.getElementById("canvas");
var ctx = canvas.getContext("2d");
ctx.fillStyle = "green";
ctx.fillRect(10, 10, 100, 100);

效果图

这是一个十分简单的例子，要获取更多关于Canvas绘图的教程，请参考文档

常用的Canvas函数

fillRect(x, y, width, height)
//绘制一个填充的矩形
strokeRect(x, y, width, height)
//绘制一个矩形的边框
clearRect(x, y, width, height)
//清除指定矩形区域，让清除部分完全透明。
beginPath()
//新建一条路径，生成之后，图形绘制命令被指向到路径上生成路径。
closePath()
//闭合路径之后图形绘制命令又重新指向到上下文中。
stroke()
//通过线条来绘制图形轮廓。
fill()
//通过填充路径的内容区域生成实心的图形。
arc(x, y, radius, startAngle, endAngle, anticlockwise)
//画一个以（x,y）为圆心的以radius为半径的圆弧，从startAngle开始到endAngle结束
//0度角为x轴正方向，anticlockwise表示顺时针(true)还是逆时针(false)

此外还有一些绘图的属性设置

fillStyle = color
//设置图形的填充颜色。
strokeStyle = color
//设置图形轮廓的颜色。
lineWidth = value
//设置线条宽度。

开始画图

本文将以制作一个加载中动画来演示如何使用Canvas绘图。

先上效果图

由图可见，整个动画是一个圆弧不断改变长度并且变色的效果。那么首先我们要先画出一个弧形来。

添加如下html标签以及JavaScript代码

<canvas id="myCanvas"></canvas>

var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d");
ctx.lineWidth = 8;
ctx.strokeStyle = "#4285f4";//线条颜色
ctx.beginPath();
ctx.arc(50, 50, 40, 0, 2/3*Math.PI);//画圆心为(50,50)半径为40的三分之一圆弧
ctx.moveTo(50, 50)
ctx.stroke();

效果图

这样就画出一个弧形。然而我们需要让它动起来，就需要动态改变圆弧的起点和终点。

var start = 0, end = 0, PI = Math.PI，
                    a = PI / 180,
                    b = PI / 50;
            //a和b分别表示圆弧起点和重点的移动速度

setInterval(function () {//这个函数表示每过15毫秒重新进行一次绘图
    var c = document.getElementById("myCanvas");
    var ctx = c.getContext("2d");

    ctx.clearRect(0, 0, 100, 100);//清空上次画出来的东西
    
    start += a;//起点和终点移动
    end += b;
    //终点比起点多转了一圈
    if (end >= start + 2 * PI) {
        end -= 2 * PI;
    }
    
    ctx.lineWidth = 8;
    ctx.strokeStyle = "#4285f4";
    ctx.beginPath();
    ctx.arc(50, 50, 40, start, end);
    ctx.moveTo(50, 50)
    ctx.stroke();
}, 15);

效果图

然而我们这始终只有一种颜色，接下来完成颜色的变化。

var start = 0, end = 0, f = true, PI = Math.PI,
        a = PI / 180,
        b = PI / 50,
        colors = {
            //定义颜色数组
            color: ["#4285f4", "#34a853", "#fbbc05", "#ea4335"],
            i: 0,
            next: function () {
                //返回下一种颜色
                return this.color[this.i++ % this.color.length];
            }
        },
        color = colors.next();

setInterval(function () {
    var c = document.getElementById("myCanvas");
    var ctx = c.getContext("2d");

    ctx.clearRect(0, 0, 100, 100);
    
    start += a;
    end += b;
    
    if (end >= start + 2 * PI) {
        end -= 2 * PI;
        f = !f;//f用来控制顺时针画弧线还是逆时
        //每转1圈换一次方向
        //每转2圈换一次颜色，
        if (f == false) {
            color = colors.next();
        }
    }
    
    ctx.lineWidth = 8;
    ctx.strokeStyle = color;
    ctx.beginPath();
    ctx.arc(50, 50, 40, start, end, f);
    ctx.moveTo(50, 50)
    ctx.stroke();
}, 15);

效果图

怎么样，是不是动画的雏形已经出来了。然而你仔细对比一下的话还会发现这动画有点太死板了。

最终效果图中的曲线并不是匀速运动的，而是开始和结束时运动慢，中间运动快。更符合我们的审美。如何制作这样的变速动画就是下一节的内容——贝塞尔曲线

贝塞尔曲线简介

贝塞尔曲线是一种在计算机里运用十分多的曲线，如Photoshop等绘图软件中的钢笔工具便是贝塞尔曲线。还有许多动画、视频运用贝塞尔曲线来控制动画速度。
下面这几幅来自维基百科的图描述了贝塞尔曲线的特点以及绘制过程。



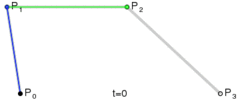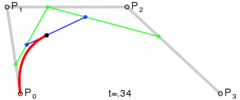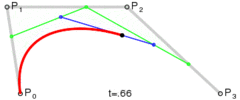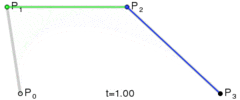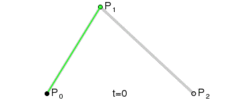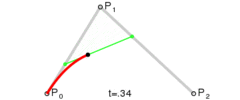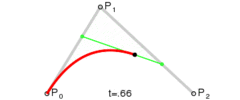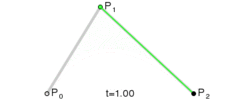
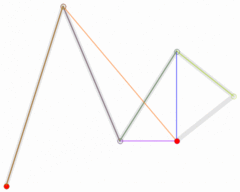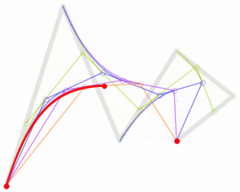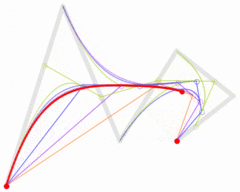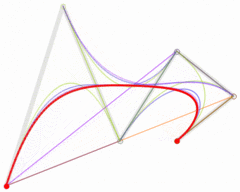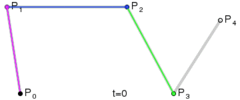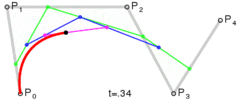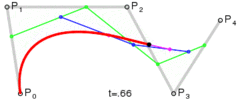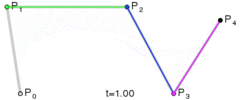
上述分别是二次贝塞尔曲线、三次贝塞尔曲线、四次贝塞尔曲线、五次贝塞尔曲线，每种贝塞尔曲线都由两个端点和几个控制点组成。比较常用的曲线一般是二次或三次的，四次以上较少用到。

当然，每种曲线都由一个计算公式。以下是二次贝塞尔曲线和三次贝塞尔曲线的计算公式



这些公式将会在等下绘制贝塞尔曲线时用到。

贝塞尔曲线在动画上的应用

有时候我们很希望一个动画是变速运动的，比如说先慢再逐渐变快，这时我们可以用贝塞尔曲线控制动画速度。


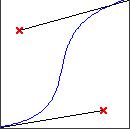
这是Gogo从MMD上截的图，很明显这是个三次贝塞尔曲线。这个图左下角为坐标(0,0)，右上角为(1,1)，两个红点是控制点。

其中横轴代表时间，纵轴代表动画完成度（%），斜率代表动画进行速度。这张图表示的就是一个开始和结束时慢，中间快的动画。

运用三次贝塞尔曲线，只要调整两个控制点的位置，就能描述一个动画进行速度是如何变换的。

计算贝塞尔曲线

知道了贝塞尔曲线控制动画速度的原理，我们就可以来做一个变速动画了。

根据三次贝塞尔曲线的公式，起点P0(0,0)，终点P3(1,1)。其中两个控制点为P1(X1,Y1),P2(X2,Y2)。
带入公式 B(t) = (1 - t) ^ 3 ( 0 , 0 ) + 3t ( 1 - 2t + t ^ 2) ( X1 , Y1 ) + 3 ( t ^ 2 - t ^ 3) ( X2 , Y2 ) + (t ^ 3) ( 1 , 1 )
整理得 B(t) = ( ( 3 X1 - 3 X2 + 1) t  ^ 3 + ( 3 X2 - 6 X1) t  ^ 2 + 3 X1 t , ( 3 Y1 - 3 Y2 + 1) t  ^ 3 + ( 3 Y2 - 6 Y1) t  ^ 2 + 3 Y1 t )

如果你嫌这个式子太长的话，只要知道B(t)的

X轴坐标为( 3 X1 - 3 X2 + 1) t  ^ 3 + ( 3 X2 - 6 X1) t  ^ 2 + 3 X1 t
Y轴坐标为( 3 Y1 - 3 Y2 + 1) t  ^ 3 + ( 3 Y2 - 6 Y1) t  ^ 2 + 3 Y1 t

由于X轴代表的是时间，Y轴代表动画进度，所以我们只需要根据 X轴坐标，求 Y轴坐标就行。

因为 X1，X2，Y1，Y2 都是已知量，那么这就是一个一元三次方程，根据 X 坐标求出 t，再把 t带入第二个式子就能求出 Y轴坐标。

   ( 3 X1 - 3 X2 + 1) t  ^ 3 + ( 3 X2 - 6 X1) t  ^ 2 + 3 X1 t = X
即 ( 3 Y1 - 3 Y2 + 1) t  ^ 3 + ( 3 Y2 - 6 Y1) t  ^ 2 + 3 Y1 t - X = 0

至于解一元三次方程Gogo也没学过，于是只好上维基百科查下求根公式。三次方程

var x1 = 0.5 , y1 = 0 , x2 = 0.5 , y2 = 1 , x = 0.5;

//Js的pow函数对负数开奇数次方没用，例如 pow( -8 , 1 / 3) 即-8的根号三，返回 NaN 而不是 -2
//因此在这里封装下pow函数，使其可以给负数开奇数次方
var pow = function (n, l) {
    if (n < 0 && l == 1 / 3) {
        return -Math.pow(-n, l);
    } else {
        return Math.pow(n, l);
    }
};
var a = 3 * x1 - 3 * x2 + 1;
var b = 3 * x2 - 6 * x1;
var c = 3 * x1;
var d = -x;
var a2 = pow(a, 2);
var a3 = pow(a, 3);
var b2 = pow(b, 2);
var b3 = pow(b, 3);
var de = pow(pow(b * c / 6 / a2 - b3 / 27 / a3 - d / 2 / a, 2) + pow(c / 3 / a - b2 / 9 / a2, 3), 1 / 2);
var de1 = pow(b * c / 6 / a2 - b3 / 27 / a3 - d / 2 / a + de, 1 / 3);
var de2 = pow(b * c / 6 / a2 - b3 / 27 / a3 - d / 2 / a - de, 1 / 3);

var t = -b / 3 / a + de1 + de2;//求出t

var ya = 3 * y1 - 3 * y2 + 1;
var yb = 3 * y2 - 6 * y1;
var yc = 3 * y1;

var y = ya * pow(t, 3) + yb * pow(t, 2) + yc * t;//带入t求出y

这样子我们就成功地根据X轴坐标(时间)求出Y轴坐标(动画进度)了。然后对我们前面那个动画进行修改。

//定义贝塞尔曲线
c3 = {	
create: function (x1, y1, x2, y2) {
return function (x) {
    var pow = function (n, l) {
        if (n < 0 && l == 1 / 3) {
            return -Math.pow(-n, l);
        } else {
            return Math.pow(n, l);
        }
    };
    var a = 3 * x1 - 3 * x2 + 1;
    var b = 3 * x2 - 6 * x1;
    var c = 3 * x1;
    var d = -x;
    var a2 = pow(a, 2);
    var a3 = pow(a, 3);
    var b2 = pow(b, 2);
    var b3 = pow(b, 3);
    var de = pow(pow(b * c / 6 / a2 - b3 / 27 / a3 - d / 2 / a, 2) + pow(c / 3 / a - b2 / 9 / a2, 3), 1 / 2);
    var de1 = pow(b * c / 6 / a2 - b3 / 27 / a3 - d / 2 / a + de, 1 / 3);
    var de2 = pow(b * c / 6 / a2 - b3 / 27 / a3 - d / 2 / a - de, 1 / 3);
    var t = -b / 3 / a + de1 + de2;
    var ya = 3 * y1 - 3 * y2 + 1;
    var yb = 3 * y2 - 6 * y1;
    var yc = 3 * y1;
    return ya * pow(t, 3) + yb * pow(t, 2) + yc * t;
    }
}
}
//得到一条控制点为( 0.5 , 0 ) , ( 0.5 , 1 )的三次贝塞尔曲线。
var fun = c3.create(0.5, 0, 0.5, 1);

var start = 0, end = 0, f = true, PI = Math.PI, i = 0, total = 60,
        a = PI / 180,
        colors = {
            color: ["#4285f4", "#34a853", "#fbbc05", "#ea4335"],
            i: 0,
            next: function () {
                return this.color[this.i++ % this.color.length];
            }
        },
        color = colors.next();
setInterval(function () {
    i = (i + 1) % total;

    var val = fun(i / total);//计算得到动画完成了百分之多少
    
    var c = document.getElementById("c2");
    var ctx = c.getContext("2d");
    ctx.clearRect(0, 0, 100, 100);
    start += a;
    start %= 2 * PI;
    end = val * 2 * PI;//根据动画完成百分比得到结束点距起点距离
    if (i == 0) {
        f = !f;
        if (f == false) {
            color = colors.next();
        }
    }
    ctx.lineWidth = 8;
    ctx.strokeStyle = color;
    ctx.beginPath();
    ctx.arc(50, 50, 40, start, start + end /*结束点位置*/ , f);
    ctx.moveTo(50, 50)
    ctx.stroke();
}, 15);

最终效果图